Типичные скорости (практические скорости) потока воздуха, газов и водяного пара в трубопроводах и вентиляционных газоходах (трубах) в различных технологичеcких и коммунальных сетях.
Проводимость канала определяет его способность транспортировать газ. Она выражается в единицах объема газа, проходящего через данное сечение в единицу времени. Зависимости для расчета проводимости элемента, работающего в различных условиях, являются весьма сложными и зависят от режима течения, а также от геометрических параметров канала и свойств его поверхности. Расчеты проводимости и потока газа при турбулентном режиме течения трудно трактовать аналитически. Количественное определение параметров вязкостного потока также представляет трудности, поскольку зависит не только от формы канала, но и от давления газа. Однако при тех диапазонах давлений, которые имеют место в условиях высокого вакуума, поток является молекулярным, а не вязкостным.
Уравнения для расчета параметров вязкостного потока
В общем случае уравнения для расчета проводимости и потока газа при вязкостном режиме течения получены для трубопроводов и каналов, имеющих сечение простой геометрической формы — круглое или прямоугольное. Эти выражения используются, например, для расчета времени, необходимого для откачки сосуда через трубопровод, имеющий круглое или прямоугольное поперечное сечение.
Течение в трубопроводах круглого сечения
Поток газа по прямому трубопроводу круглого сечения в условиях вязкостного режима определяется уравнением Пуазейля:
где d — диаметр трубы; L — длина трубопровода; η — динамическая вязкость газа; р — среднее давление в трубопроводе; р1 и р2 — давления на противоположных концах трубы.
Для сухого воздуха при 20 °С данное уравнение приобретает вид:
где Q — поток газа, Торр — л/с; d — диаметр трубопровода, см; L — длина трубопровода, см; р — это давление, Торр.
Проводимость круглого трубопровода, л/с, для воздуха при 20 °С приведено ниже:
Течение в прямоугольных каналах
Уравнение Пуазейля для потока воздуха при 20 °С, текущего по прямоугольному каналу с большей стороной сечения а и меньшей b, имеет следующий вид, л/с:
где К — это коэффициент формы, значение которого зависит от b/а.
Как можно видеть, проводимость прямоугольной диафрагмы (отверстия) быстро увеличивается при переходе сечения от прямоугольной щели к квадрату.
Так же, как и в случае круглого трубопровода, выражение для С позволяет получить соотношение для объемного потока газа в зависимости от перепада давлений в канале.
Уравнения для расчета параметров молекулярного потока
При низких значениях давления межмолекулярные столкновения происходят реже, чем столкновения со стенкой, поэтому последние определяют параметры газового потока по каналу. Проводимость канала в условиях молекулярного потока зависит от двух факторов:
- Скорости, с которой молекулы поступают в канал.
- Вероятности прохождения молекул по системе.
Первый фактор зависит от площади сечения входа в систему, а последний определяется последующей серией столкновений со стенками, в результате которых молекула в конечном итоге перемещается по каналу или отбрасывается обратно в откачиваемый сосуд.
Рассмотрим вначале случай очень тонкой диафрагмы в пластине. В данном случае для определения проводимости диафрагмы нас интересует ее площадь А, а не свойства стенок канала. Объем газа, проходящего через диафрагму — ее проводимость — составляет:
если молекулы имеют распределение скоростей по Максвеллу. Значения проводимости зависят от молекулярной массы и кинетической энергии. Случай, когда столкновения молекул со стенками трубопровода являются более важными, чем проводимость отверстия, рассмотрен ниже.
Формула Кнутсена
Проводимость СΥотрезка длинной трубы длиной L с переменной площадью сечения А и периметром Н была рассчитана Кнудсеном и составляет:
Были приняты следующие допущения:
- Длина трубопровода значительно больше диаметра.
- Направление движения отскочивших молекул после столкновения со стенками не зависит от направления их движения до столкновения.
- Угловое распределение отскочивших молекул подчиняется закону косинуса.
Допущение 1 предполагает, что влияние отверстия является незначительным, а величина проводимости, получаемая из уравнения (67), относится к молекулам внутри трубы, удаленным от отверстия. Для получения приближенных выражений для проводимости всей трубы нужно включить последовательную проводимость отверстий. Карлсон приводит формулу для трубопровода с периметром Н, площадью Л и длиной L:
Коэффициент Клаузинга
Проводимость длинного трубопровода связана с проводимостью входного отверстия коэффициентом [1 +3/16(LH/A)] -1 Ca. Этот коэффициент можно интерпретировать как вероятность случайного входа молекулы в отверстие и ее прохождения до самого конца трубопровода.
Целесообразно рассматривать проводимость с точки зрения проводимости отверстия и соответствующей вероятности прохождения молекулы (коэффициента Клаузинга), поэтому
Так как проводимость не зависит от направления движения молекул,
Примеры. Выражение для потока газа по длинному прямому трубопроводу было дано Кнудсеном:
где d — диаметр трубопровода; L — длина трубопровода; nа — средняя скорость молекулы; р1 и р2 — давления на противоположных концах трубопровода.
Для сухого воздуха при 20 °С d и L, выраженных в дюймах, а р — в Торр, данное уравнение принимает следующий вид:
Приблизительные значения некоторых вероятностей прохождения имеют точность в пределах + 10%. Это разнообразные методы, которые включают аналитические методы, расчеты по методу пробной частицы Монте-Карло и методу вариаций. Карлсон исследовал различные геометрические формы и ссылается на соответствующие источники. Примеры числовых расчетов можно найти в работе Карлсона.
Читайте также Как соединить трубы без сварки при помощи муфты Гебо
Группа РОСВАКУУМ
Адрес: 107023 Россия, г. Москва, Электрозаводская улица, 21
Часы работы офиса: с 9:00 до 18:00 по Москве.
Телефон: +7 (495) 664-22-07
E-mail: baza@vacuumpro.ru
Чтобы заказать бесплатный подбор оборудования, отправить заявку, запрос или получить консультацию инженеров — свяжитесь с нами по телефону или E-mail.
В базе 310 производителей и поставщиков вакуумного оборудования и техники (РФ, СНГ и зарубежные компании). Цены, наличие на складах и технические характеристики оборудования и техники уточняйте только по электронной почте E-mail.
Типичные скорости (практические скорости) потока воздуха, газов и водяного пара в трубопроводах и вентиляционных газоходах (трубах) в различных технологичеcких и коммунальных сетях.
Типичные скорости (практические скорости) потока воздуха, газов и водяного пара в трубопроводах и вентиляционных газоходах (трубах) в различных технологичеcких и коммунальных сетях.
Комфортной (не вызывающей излишней коррозии / эрозии или шума в трубопроводах) считается скорость до 7 м/с для газопроводов низкого давления, 15 м/с для газопроводов среднего давления, 25 м/с для газопроводов высокого давления (для простоты — «без серьезного приборного давления», «с приборным порядка единиц атмосфер», «с приборным давлением выше 3 бар»). Приемлемой на практике (уже будет шумно)- до 50-100 м/с. А практически встречающиеся скорости см. в таблице ниже:
Дополнительная информация: «. Скорость потока учитывается только для определения диаметра трубопровода. При неправильном выборе диаметра (скорость потока для: жидкой среды от 3 до 10 м/с; газообразной — свыше 20 м/с) будет наблюдаться повышенная вибрация трубопровода и образование статического электричества. Кавитация от скорости не зависит, а только от перепада давления и давления насыщенных паров перекачиваемой жидкости.» ТПА номер 5(86) 2016 г — Якименко В.К. ЗАО «ТюменьВНИПИнефть»

Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Скорость течения газа в трубе. Движение газа по трубам. Основные положения и задачи
Резкое увеличение давления, сопровождающее гидравлический удар — явление крайне негативное, т.к. гидравлический удар может разрушить трубопровод или какие-либо элементы гидравлических машин, испытывающие эффекты гидравлического удара. По этой причине разрабатываются методы предотвращения гидравлических ударов или уменьшить его негативное влияние. Поскольку мощность гидравлического удара напрямую зависит от массы движущийся жидкости, то для предотвращения гидравлического удара следует максимально уменьшить массу жидкости, которая будет участвовать в гидравлическом ударе. Для этого необходимо запорную арматуру монтировать в непосредственной близости к резервуару. В качестве меры уменьшения негативных последствий гидравлического удара используют замену прямого гидравлического удара на непрямой. Для этого достаточно запорную арматуру на напорных трубопроводах сделать медленно закрывающейся, что позволит уменьшить силу удара. Другой мерой борьбы с
явлением гидравлического удара является установка на напорных линиях, работающих в условиях
циклической нагрузки специальных компенсаторов с воздушной подушкой, которая принимает на себя удар
Однако в ряде случаев явление гидравлического удара успешно используется. К таким случаям использования гидравлического удара относятся производственные процессы по разрушению материалов и др. Известна специальная конструкция водоподъёмника, базирующаяся на использовании гидравлического удара.
Основной отличительной особенностью движения газа по трубам от движения капельных жидкостей заключается в том, что капельные жидкости характеризуются весьма малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства практических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости. При движении газа таких допущений делать нельзя. Поскольку изучение общих решений уравнений газодинамики не является предметом настоящего курса, рассмотрим лишь частные задачи, встречающиеся в практике работы специалистов горных отраслей промышленности. К числу таких первоочередных задач относится изучение движения газов, включая воздух по газопроводам (воздуховодам).
Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных потерь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неодинаковы в различных сечениях газопровода. Рассмотрим наиболее простой случай газопровода (воздуховода) собранного из труб одинакового диаметра (простой газопровод S = const ) при установившемся движении газа. Тогда в соответствии с уравнением неразрывности потока газа массовый расход газа вдоль газопровода является величиной постоянной= const. При этом объёмный расход газа будет меняться от одного сечения газопровода к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется.
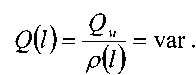
Тогда скорость движения газа также будет меняться вдоль длины газопровода:
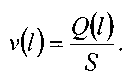
При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движение газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = const и= const. При таких условиях будет посто-
янным для всего потока и число Рейнольдса, и как следствие будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
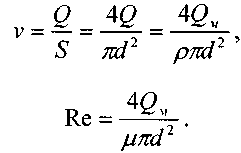
Отметим, что в последнем выражении все величины, входящие в правую часть равенства являются величинами постоянными, отсюда: Re = const и /I = const. По этой причине для определения величины потерь напора и расхода газа можно воспользоваться обычным уравнением Бернулли.
10.2. Основные уравнения газодинамики для установившегося движения газа в простом газопроводе
Читайте также Какой газ используется в жилых домах
Запишем уравнение Бернулли в дифференциальной форме:
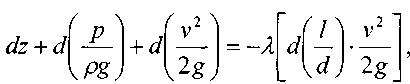
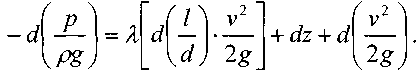
Последний член уравнения весь мал и его величиной можно пренебречь, тогда для горизонтального газопровода (z = const ) можно записать:
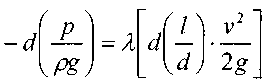
Подставив в последнее уравнение значение средней скорости движения газа, выразив её через массовый расход, получим:
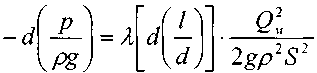
По принятым выше условиям процесс движения газа по газопроводу является изотермическим, тогда подставив в последнее уравнение значение из уравнения Бойля-Мариотта:
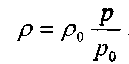
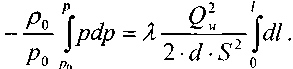
Решая последнее уравнение, получим основные расчётные формулу для определения потерь давления в газопроводе и формулу для определения массового расхода газа в газопроводе.
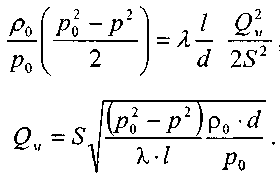
Величина коэффициента трения Л определяется по формулам для жидкости в зависимости от режима её движения или же можно воспользоваться эмпирической формулой ВННИИГаза:
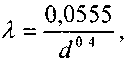
где d- диаметр газопровода в сантиметрах.
Для приближенного расчета движения жидкости или газа по трубам можно отвлечься от весьма сложных деталей этого движения (об этом будет сказано в заключительных главах) и удовольствоваться следующей упрощенной схемой. Примем поток за одномерный, т. е. будем пренебрегать изменением величины и направления скорости, а также изменениями других элементов потока (давления, плотности, температуры и др.) по сечению, перпендикулярному к оси потока; будем лишь учитывать изменение средних по сечениям величин и др. в зависимости от координаты х, определяющей положение сечения вдоль оси трубы. Площадь сечения А будем считать заданной функцией х. Отвлечемся от сил трения внутри жидкости и жидкости о стенку, а также от теплопроводности; иными словами, как повсюду в настоящей главе, будем считать жидкость идеальной.
Начнем с простейшего случая — движения несжимаемой жидкости.
В этом случае из уравнения неразрывности сразу следует
где средняя скорость в некотором начальном сечении с площадью иными словами, средняя скорость движения жидкости в любом сечении трубы обратно пропорциональна площади этого сечения.
Отсюда вытекает общеизвестное свойство движения несжимаемой жидкости по трубе переменного сечения: в сужающейся трубе жидкость движется ускоренно, в расширяющейся — замедленно.
Это очевидное свойство одномерного движения теряет свою силу при движении сжимаемого газа со сверхзвуковыми скоростями, в чем легко убедиться, составив основные уравнения одномерного стационарного движения газа:
а) уравнение Эйлера:
б) уравнение неразрывности:
Вспоминая определение местной скорости звука
перепишем уравнение Эйлера (83) в виде:
Составляя логарифмический дифференциал от обеих частей равенства (84), получим:
Исключая — из уравнений (85) и (86), найдем:
или, вводя местное число
Из этого простого уравнения вытекают важные следствия:
1. Если знак противоположен знаку т. е. при дозвуковом движении газа сохраняется то же свойство движения, что и в случае несжимаемой жидкости: с возрастанием площади сечения трубы скорость в одномерном движении уменьшается и, наоборот, при уменьшении сечения — скорость увеличивается.
2. Если знак одинаков со знаком т. е. при сверхзвуковом движении газа в сужающейся трубе движение замедляется, в расширяющейся трубе — ускоряется. Этот парадоксальный на первый взгляд результат объясняется тем, что при расширении газа плотность его настолько сильно уменьшается, что произведение в равенстве (84), несмотря на увеличение площади А, все же уменьшается и приводит к возрастанию скорости и.
3. Если Сечение трубы, в котором число достигает значения единицы, называется критическим сечением, так как в нем скорость движения и равна местной скорости звука а. Из равенства (87) следует, что критическое сечение может быть максимальным, так и минимальным по сравнению со смежными сечениями. Легко сообразить, что критическое сечение будет минимальным, так как при подходе к максимальному сечению дозвуковой поток замедляется, а сверхзвуковой ускоряется, что никак не может привести к течению со скоростью звука в критическом сечении.
Если и сечение экстремально (максимально или минимально), то по (87) либо следовательно, это сечение —
критическое, либо В последнем случае, каково бы ни было движение — дозвуковое или сверхзвуковое — скорость в экстремальном сечении принимает также экстремальное значение; при дозвуковом течении газа — минимальное в максимальном сечении и максимальное в минимальном сечении, при сверхзвуковом течении, наоборот, в максимальном сечении скорость максимальна, в минимальном — минимальна.
Переходя к более детальному изучению одномерного адиабатического и изэнтропического движения газа, заметим, что к нему применимы все ранее выведенные соотношения, связывающие между собою термодинамические параметры газа и скорость движения или число Необходимо только установить связь между одним каким-нибудь из этих параметров и сечением трубы А.
Примем за основную, например, связь между Чтобы вывести уравнение этой связи возьмем уравнение
получаемое логарифмическим дифференцированием равенства
и уравнение Бернулли в форме (47):
которое после дифференцирования дает
или, после делении обеих частей на и замены
Подставляя это значение в (88), получим
Сравнивая это уравнение с уравнением (87), будем иметь:
Уравнение это нетрудно проинтегрировать и получить искомое уравнение связи между числом и площадью сечения А:
где произвольное начальное сечение трубы и число в этом сечении.
Предположим, что роль начального сечения играет критическое сечение т. е. такое сечение, в котором тогда равенство (89) приводится к более простому виду:
На рис. 47 приведен график этой важной зависимости для воздуха График подтверждает ранее отмеченный факт: в дозвуковом потоке для увеличения числа сечение А следует уменьшать, в сверхзвуковом потоке наоборот, увеличивать; вместе с тем график показывает количественное соотношение между изменениями чисел
Так, например, из рис. 47 следует, что для повышения числа от 0,2 до 0,8 газ должен пройти через участок суживающейся трубы-конфузора с сечением, уменьшающимся в три раза; чтобы увеличить число от значения 1 в критическом сечении до 3,2, необходимо построить расширяющуюся трубу-диффузор — с площадью на выходе, в пять раз превышающей площадь критического сечения.
Читайте также Опоры и подвески трубопроводов
Присоединим к формуле (90) известные уже по предыдущему формулы (69), (70), (66) изэнтропической связи давления, плотности и температуры с числом которые, в силу (51) и (52) полезно
переписать в виде:
Совокупность равенств (90) и (91) представляет полное решение задачи об одномерном стационарном адиабатическом и изэнтропическом движении газа по трубе переменного сечения; решение это представлено в удобном параметрическом виде, причем роль параметра играет число Задавшись законом изменения площади сечения трубы определим по (90), а затем и искомые по (91).
Из уравнения неразрывности или сохранения массы (84) следует, что при наличии в одномерном потоке критического сечения будет существовать соотношение
представляет отношение массового расхода газа через единицу площади сечения трубы к его критическому значению. Этот безразмерный массовый расход данного газа является функцией только числа согласно (90), равен:
График зависимости от для воздуха приведен на том же рис. 47.
В качестве первого примера приложения выведенных формул рассмотрим классическую задачу об изэнтропическом истечении газа из резервуара (котла) очень большой вместимости.
Предположим сначала, что сопло, из которого происходит истечение, имеет вид конфузора, т. е. канала с уменьшающимся вниз по потоку сечением. Обозначим через термодинамические параметры газа в котле, где газ, в силу большой вместимости котла, может рассматриваться как покоящийся через соответствующие параметры в выходном сечении, площадь которого
пусть будет А, и через давление в среде, куда происходит истечение; это давление в теории истечения называют противодавлением.
Определим прежде всего основную характеристику одномерного потока в целом — секундный массовый расход газа одинаковый для всех сечений потока и равный
или, на основании формул (52):
При заданных параметрах газа в котле и геометрической форме сопла секундный массовый расход газа является функцией только числа в выходном сечении, определяемой выражением в формуле (93). Что касается выходного числа то оно, в силу принятой наперед адиабатичности и изэнтропичности потока, определяется заданием давления на выходе согласно известной формуле (69):
Определяя отсюда в функции от и подставляя это значение в выражение в, получим после простых приведений формулу:
представляющую, очевидно, простое приложение ранее указанной формулы Сен-Венана и Ванцеля [(67) гл. III].
Пользуясь одновременно формулами (94) и (95), легко исследовать изменение секундного массового расхода истечения в функции отпротиводавления которое при совпадает практически с или числа в выходном сечении.
При движении газа на каждый его объем будут действовать не только те силы, которые характерны для статики, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеального газа этими дополнительными силами будут силы инерции, а для реального газа — силы инерции и трения (вязкости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих математических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье — Стокса). Уравнения Навье — Стокса настолько сложны, что к настоящему времени решены лишь для крайне ограниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Таким образом, получено одно из важнейших уравнений гидро- и аэродинамики — уравнение (закон) Бернулли.
Уравнение Бернулли.
В практических условиях распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизменным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).
Для несжимаемого газа () уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид
В соответствии с этим величина является пьезометрическим давлением, величина
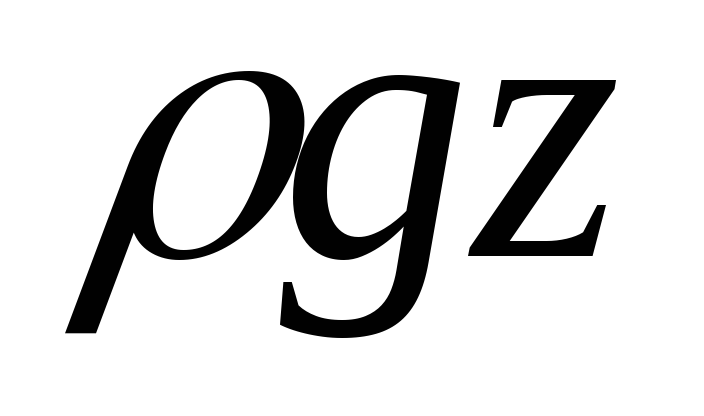
— геометрическим давлением, величина
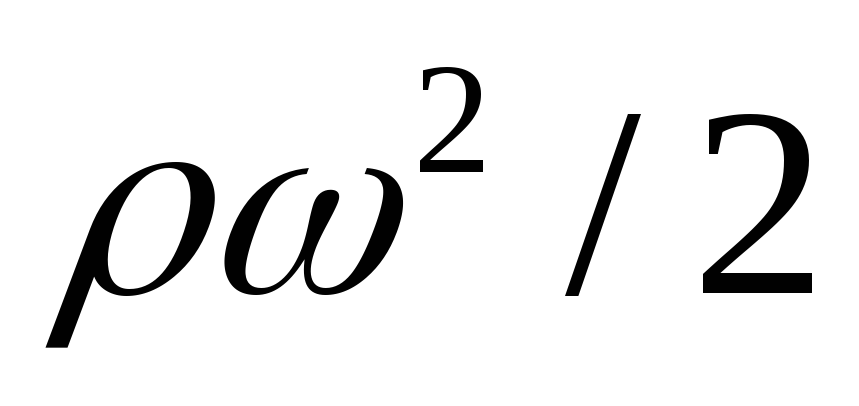
Уравнение Бернулли представляет собой закон сохранения энергии, поскольку сумма
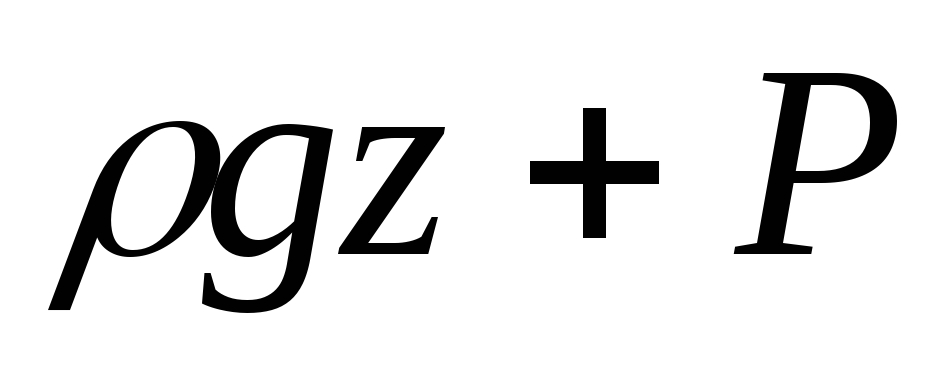
характеризует потенциальную, а величина
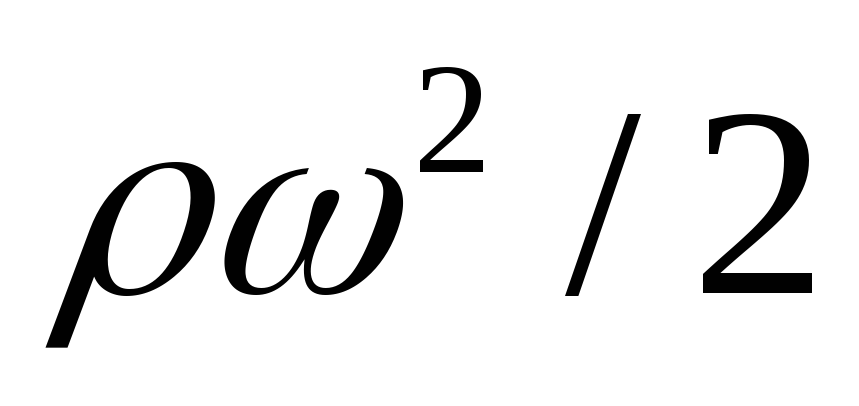
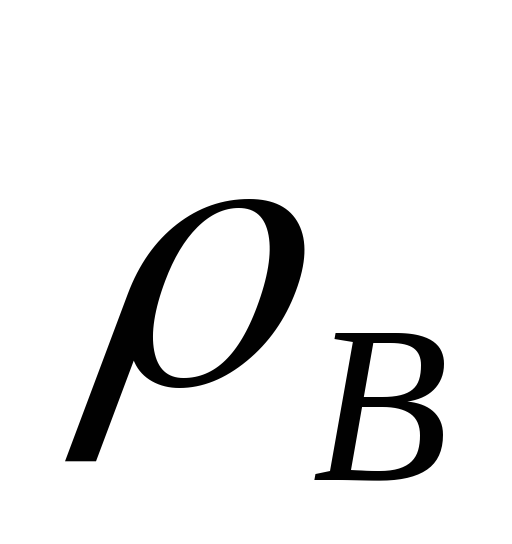
В металлургической теплотехнике в большинстве случаев пользуются давлением, избыточным над атмосферным. Необходимо уравнение Бернулли привести к такому виду, при котором все члены его были бы выражены в избыточных давлениях. Для этого представим себе канал, окруженный воздухом плотностью , по которому движется газ плотностью
. Принимая плотности газа и воздуха неизменными, напишем уравнение Бернулли и для газа и воздуха применительно к сечениям канала и .
Уравнение для газа
Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)
Вычитая из первого второе, получаем уравнение Бернулли для газа в избыточных давлениях:
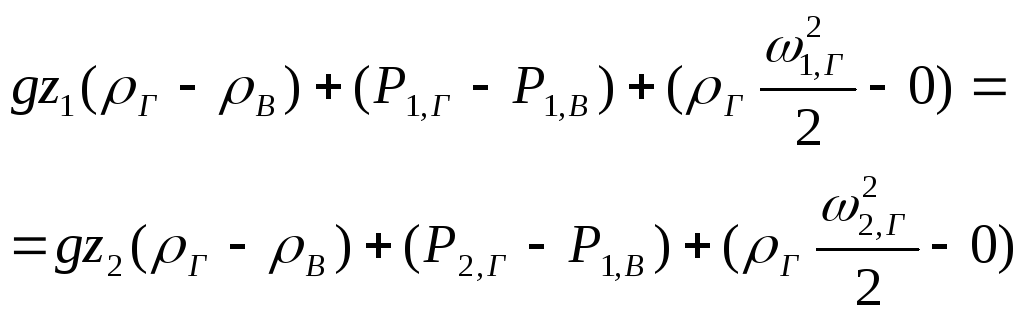
Уравнение можно переписать в таком виде:
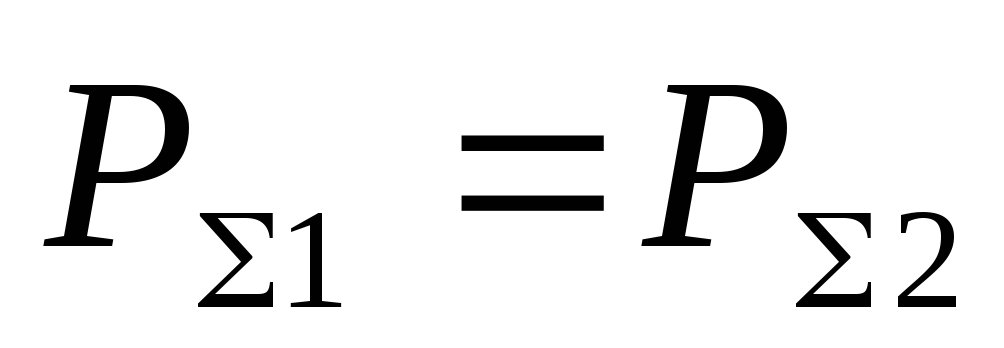
строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Если по каналу перемещается реальная (вязкая) жидкость (газ), то часть энергии тратится на преодоление трения и различных сопротивлений и происходит потеря энергии.
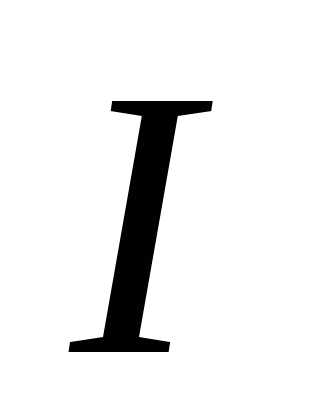
В этом случае при движении от сечення к сечению
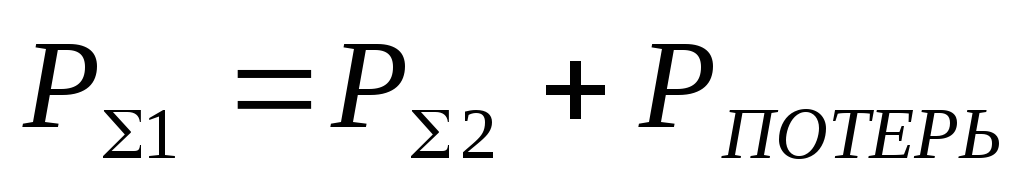
и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жидкости (газа) для различных сечений канала сумма давлений всех видов является постоянной».
Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли.
При движении реального газа часть его энергии расходуется на преодоление трения и различных сопротивлений.
Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при повороте канала или усложнении его сечения, при соударении потоков. Величину потерь энергии выражают в долях скоростного давления.
Потери на трение

,(Па) можно определить по формуле
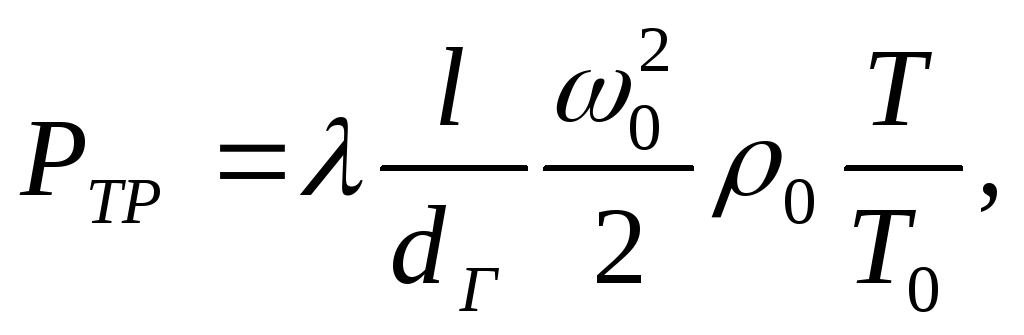
где — коэффициент трения; — длина канала, м; — гидравлический диаметр канала, м; и — плотность и скорость жидкости (газа) при нормальных условиях, т.е. при атмосферном давлении и температуре Т о , равной 273 К; Т — действительная температура жидкости или газа, К.
Похожие записи:
- Труба защитная гибкая гофрированная из полимера и нержавейки
- Фланцевые задвижки — конструкция, виды, характеристики
- Диаметры задвижек: фланцевых, чугунных, шиберных, клиновых
- Задвижка с обрезиненным клином 30ч39р — характеристики, применение
https://enersb.ru/komplektujushhie-dlya-truboprovodov/tipichnye-skorosti-prakticheskie-skorosti-potoka-vozduha-gazov-i-vodyanogo-para-v-truboprovodah-i-ventilyacionnyh-gazohodah-trubah-v-razlichnyh-tehnologicheckih-i-kommunalnyh-setyah/
